Step-by-Step Guide to Calculating Standard Error in Excel
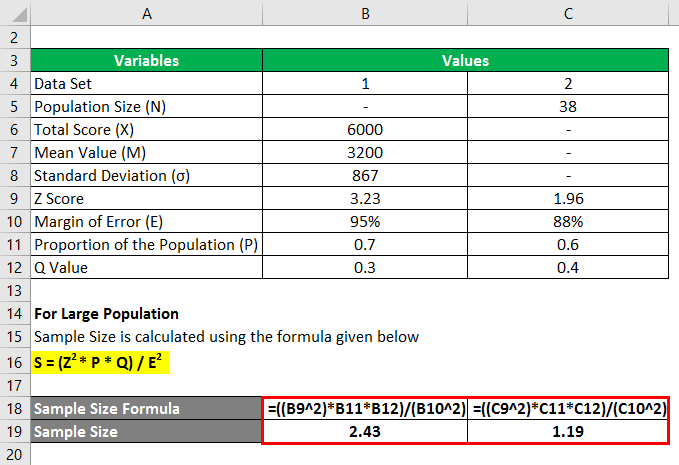
Calculating the standard error of a dataset is an essential task in statistics, particularly when analyzing the reliability of sample data. Excel, with its powerful statistical functions, makes it easy to compute the standard error. This guide will walk you through a detailed, step-by-step process for calculating the standard error in Excel, complete with visual aids and examples.
1. What is Standard Error and Why is it Important?
The standard error (SE) measures the accuracy with which a sample distribution represents a population by using the standard deviation of the sample mean. It indicates how much the sample mean is likely to fluctuate from the true population mean.
Key Points about Standard Error:
- A smaller standard error suggests that the sample mean is a more accurate reflection of the actual population mean.
- Standard error is commonly used in inferential statistics, such as hypothesis testing and confidence intervals.
Understanding the concept of standard error helps in interpreting statistical results and making informed decisions based on data analysis.
2. The Formula for Calculating Standard Error
The standard error can be calculated using the following formula:
SE=snSE = \frac{s}{\sqrt{n}}
where:
- ss is the standard deviation of the sample.
- nn is the number of observations in the sample.
To calculate the standard error in Excel, you first need to compute the standard deviation and then divide it by the square root of the sample size.
3. Step-by-Step Guide to Calculate Standard Error in Excel
Let’s walk through the process of calculating the standard error in Excel using a sample dataset.
Step 1: Prepare Your Data
Ensure that your data is organized in a single column or row in an Excel worksheet. For this example, let’s assume you have a sample dataset in column A (A1
).
Example Data:
| A |
|---|
| 5.2 |
| 4.8 |
| 6.1 |
| 5.7 |
| 4.9 |
| 5.3 |
| 5.6 |
| 6.0 |
| 5.8 |
| 5.5 |
Step 2: Calculate the Standard Deviation
To calculate the standard error, you first need the standard deviation of your sample data.
Formula to Use:
=STDEV.S(range)\text{=STDEV.S(range)}
Instructions:
- Click on an empty cell where you want the standard deviation to be displayed.
- Enter the formula:
=STDEV.S(A1:A10)and pressEnter.
Excel will calculate and display the standard deviation of your sample data.
Step 3: Calculate the Sample Size
Next, determine the number of observations (sample size) in your dataset.
Formula to Use:
=COUNT(range)\text{=COUNT(range)}
Instructions:
- Click on another empty cell.
- Enter the formula:
=COUNT(A1:A10)and pressEnter.
Excel will return the total number of observations in the dataset.
Step 4: Calculate the Standard Error
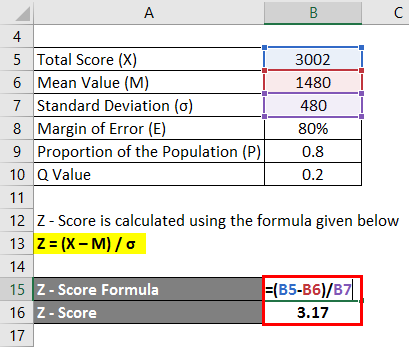
Now that you have both the standard deviation and the sample size, you can calculate the standard error.
Formula to Use:
=STDEV.S(range) / SQRT(COUNT(range))\text{=STDEV.S(range) / SQRT(COUNT(range))}
Instructions:
- Click on a new empty cell where you want the standard error to appear.
- Enter the formula:
=STDEV.S(A1:A10) / SQRT(COUNT(A1:A10))and pressEnter.
Excel will calculate and display the standard error for your dataset.
4. Using the Data Analysis Toolpak for Standard Error Calculation
Excel’s Data Analysis Toolpak offers a more advanced approach for statistical analysis, including calculating the standard error.
How to Enable the Data Analysis Toolpak:
- Go to File > Options > Add-Ins: Select “Excel Add-ins” and click “Go.”
- Check “Analysis ToolPak”: Ensure the checkbox for “Analysis ToolPak” is selected and click “OK.”
Steps to Use Data Analysis Toolpak:
- Click on the “Data” tab: Go to the “Data Analysis” button in the Analysis group.
- Select “Descriptive Statistics”: Choose the input range (your data) and check the “Summary statistics” box.
- View Output: The output will display the standard error along with other descriptive statistics.
5. Understanding the Results and Implications of Standard Error
Once you have the standard error, you can interpret the variability of your sample mean relative to the population mean. A smaller standard error indicates more precise estimates, which is crucial for making reliable statistical inferences.
Applications of Standard Error:
- Confidence Intervals: Standard error is used to construct confidence intervals around the sample mean.
- Hypothesis Testing: It is also used to determine the significance of results in hypothesis testing.
Understanding these applications helps in drawing meaningful conclusions from your data analysis.
Conclusion
Calculating the standard error in Excel is straightforward using built-in functions like STDEV.S and SQRT. By following the steps outlined in this guide, you can accurately compute the standard error of your dataset, enabling you to analyze data with greater precision and confidence.
Whether you are preparing data for reporting, conducting hypothesis testing, or constructing confidence intervals, knowing how to calculate and interpret standard error is a valuable skill in Excel. For more advanced statistical analysis, consider using Excel’s Data Analysis Toolpak or exploring additional statistical tools. If you need further assistance, don’t hesitate to reach out to Microsoft Support or consult Excel’s help resources.
